第四章:分类
原文:http://guidetodatamining.com/chapter-4
在上几章中我们使用用户对物品的评价来进行推荐,这一章我们将使用物品本身的特征来进行推荐。这也是潘多拉音乐站所使用的方法。
内容:
- 潘多拉推荐系统简介
- 特征值选择的重要性
- 示例:音乐特征值和邻域算法
- 数据标准化
- 修正的标准分数
- Python代码:音乐,特征,以及简单的邻域算法实现
- 一个和体育相关的示例
- 特征值抽取方式一览
根据物品特征进行分类
前几章我们讨论了如何使用协同过滤来进行推荐,由于使用的是用户产生的各种数据,因此又称为社会化过滤算法。比如你购买了Phoenix专辑,我们网站上其他购买过这张专辑的用户还会去购买Vampire的专辑,因此会把它推荐给你;我在Netflix上观看了Doctor Who,网站会向我推荐Quantum Leap,用的是同样的原理。我们同时也讨论了协同过滤会遇到的种种问题,包括数据的稀疏性和算法的可扩展性。此外,协同过滤算法倾向于推荐那些已经很流行的物品。试想一个极端的例子:一个新乐队发布了专辑,这张专辑还没有被任何用户评价或购买过,那它将永远不会出现在推荐列表中。
这类推荐系统会让流行的物品更为流行,冷门的物品更无人问津。
-- Daniel Fleder & Kartik Hosanagar 2009 《推荐系统对商品分类的影响》
这一章我们来看另一种推荐方法。以潘多拉音乐站举例,在这个站点上你可以设立各种音乐频道,只需为这个频道添加一个歌手,潘多拉就会播放和这个歌手风格相类似的歌曲。比如我添加了Phoenix乐队,潘多拉便会播放El Ten Eleven的歌曲。它并没有使用协同过滤,而是通过计算得到这两个歌手的音乐风格是相似的。其实在播放界面上可以看到推荐理由:
“根据你目前告知的信息,我们播放的这首歌曲有着相似的旋律,使用了声响和电音的组合,即兴的吉他伴奏。”在我的Hiromi音乐站上,潘多拉会播放E.S.T.的歌曲,因为“它有着古典爵士乐风,一段高水准的钢琴独奏,轻盈的打击乐,以及有趣的歌曲结构。”
潘多拉网站的推荐系统是基于一个名为音乐基因的项目。他们雇佣了专业的音乐家对歌曲进行分类(提取它们的“基因”)。这些音乐家会接受超过150小时的训练,之后便可用20到30分钟的时间来分析一首歌曲。这些乐曲特征是很专业的:

这些专家要甄别400多种特征,平均每个月会有15000首新歌曲,因此这是一项非常消耗人力的工程。
注意:潘多拉的音乐基因项目是商业机密,我不曾了解它的任何信息。下文讲述的是如何构造一个类似的系统。
特征值选取的重要性
假设潘多拉会用曲风和情绪作为歌曲特征,分值如下:
- 曲风:乡村1分,爵士2分,摇滚3分,圣歌4分,饶舌5分
- 情绪:悲伤的1分,欢快的2分,热情的3分,愤怒的4分,不确定的5分
比如James Blunt的那首You're Beautiful是悲伤的摇滚乐,用图表来展示它的位置便是:
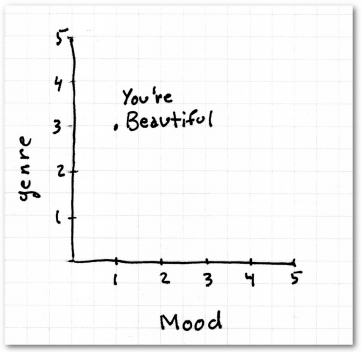
比如一个叫Tex的用户喜欢You're Beautiful这首歌,我们想要为他推荐歌曲。

我们的歌曲库中有另外三首歌:歌曲1是悲伤的爵士乐;歌曲2是愤怒的圣歌;歌曲3是愤怒的摇滚乐。你会推荐哪一首?
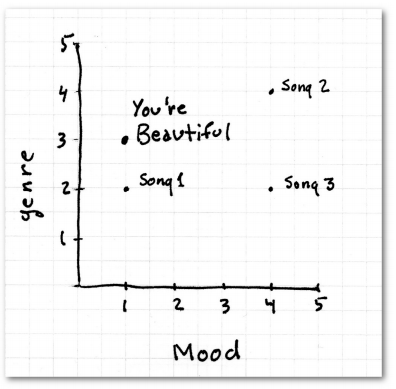
图中歌曲1看起来是最相近的。也许你已经看出了这种算法中的不足,因为不管用何种计算距离的公式,爵士乐和摇滚乐是相近的,悲伤的乐曲和快乐的乐曲是相近的等等。即使调整了分值的分配,也不能解决问题。这就是没有选取好特征值的例子。不过解决的方法也很简单,我们将每种歌曲类型拆分成单独的特征,并对此进行打分:

“乡村音乐”一栏的1分表示完全不是这个乐曲风格,5分则表示很相符。这样一来,评分值就显得有意义了。如果一首歌的“乡村音乐”特征是4分,另一首是5分,那我们可以认为它们是相似的歌曲。
其实这就是潘多拉所使用的特征抽取方法。每个特征都是1到5分的尺度,0.5分为一档。特征会被分到不同的大类中。通过这种方式,潘多拉将每首歌曲都抽象成一个包含400个数值元素的向量,并结合我们之前学过的距离计算公式进行推荐。
一个简单的示例
我们先来构建一个数据集,我选取了以下这些特征(可能比较随意),使用5分制来评分(0.5分一档):
- 使用钢琴的程度(Piano):1分表示没有使用钢琴,5分表示整首歌曲由钢琴曲贯穿;
- 使用美声的程度(Vocals):标准同上
- 节奏(Driving beat):整首歌曲是否有强烈的节奏感
- 蓝调(Blues infl.)
- 电音吉他(Dirty elec. Guitar)
- 幕后和声(Backup vocals)
- 饶舌(Rap infl.)
使用以上标准对一些歌曲进行评分:
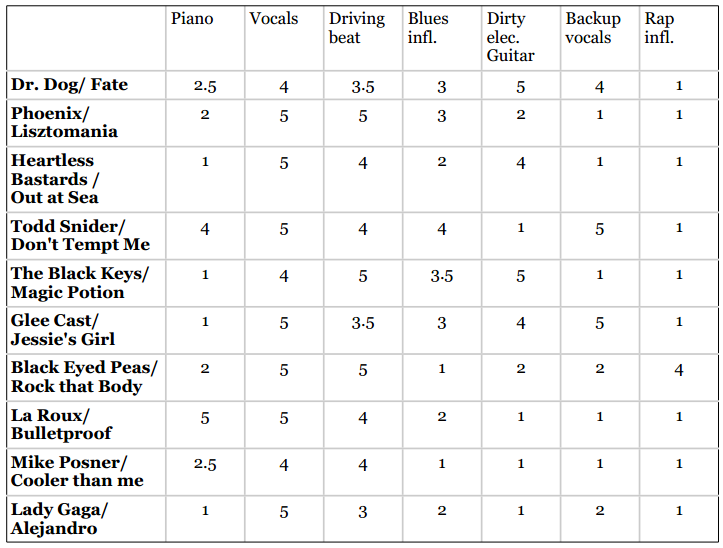
然后我们便可以使用距离计算公式了,比如要计算Dr. Dog的Fate歌曲和Phoenix的Lisztomania之间的曼哈顿距离:

相加得到两首歌曲的曼哈顿距离为9。
使用Python实现推荐逻辑
回忆一下,我们在协同过滤中使用的用户评价数据是这样的:
users = {"Angelica": {"Blues Traveler": 3.5, "Broken Bells": 2.0, "Norah Jones": 4.5, "Phoenix": 5.0, "Slightly Stoopid": 1.5, "The Strokes": 2.5, "Vampire Weekend": 2.0},
"Bill":{"Blues Traveler": 2.0, "Broken Bells": 3.5, "Deadmau5": 4.0, "Phoenix": 2.0, "Slightly Stoopid": 3.5, "Vampire Weekend": 3.0}}
我们将上文中的歌曲特征数据也用类似的格式储存起来:
music = {"Dr Dog/Fate": {"piano": 2.5, "vocals": 4, "beat": 3.5, "blues": 3, "guitar": 5, "backup vocals": 4, "rap": 1},
"Phoenix/Lisztomania": {"piano": 2, "vocals": 5, "beat": 5, "blues": 3, "guitar": 2, "backup vocals": 1, "rap": 1},
"Heartless Bastards/Out at Sea": {"piano": 1, "vocals": 5, "beat": 4, "blues": 2, "guitar": 4, "backup vocals": 1, "rap": 1},
"Todd Snider/Don't Tempt Me": {"piano": 4, "vocals": 5, "beat": 4, "blues": 4, "guitar": 1, "backup vocals": 5, "rap": 1},
"The Black Keys/Magic Potion": {"piano": 1, "vocals": 4, "beat": 5, "blues": 3.5, "guitar": 5, "backup vocals": 1, "rap": 1},
"Glee Cast/Jessie's Girl": {"piano": 1, "vocals": 5, "beat": 3.5, "blues": 3, "guitar":4, "backup vocals": 5, "rap": 1},
"La Roux/Bulletproof": {"piano": 5, "vocals": 5, "beat": 4, "blues": 2, "guitar": 1, "backup vocals": 1, "rap": 1},
"Mike Posner": {"piano": 2.5, "vocals": 4, "beat": 4, "blues": 1, "guitar": 1, "backup vocals": 1, "rap": 1},
"Black Eyed Peas/Rock That Body": {"piano": 2, "vocals": 5, "beat": 5, "blues": 1, "guitar": 2, "backup vocals": 2, "rap": 4},
"Lady Gaga/Alejandro": {"piano": 1, "vocals": 5, "beat": 3, "blues": 2, "guitar": 1, "backup vocals": 2, "rap": 1}}
假设我有一个朋友喜欢Black Keys Magic Potion,我便可根据曼哈顿距离来进行推荐:
>>> computeNearestNeighbor('The Black Keys/Magic Potion', music)
[(4.5, 'Heartless Bastards/Out at Sea'), (5.5, 'Phoenix/Lisztomania'), (6.5, 'Dr Dog/Fate'), (8.0, "Glee Cast/Jessie's Girl"), (9.0, 'Mike Posner'), (9.5, 'Lady Gaga/Alejandro'), (11.5, 'Black Eyed Peas/Rock That Body'), (11.5, 'La Roux/Bulletproof'), (13.5, "Todd Snider/Don't Tempt Me")]
这里我推荐的是Heartless Bastard的Out as Sea,还是很合乎逻辑的。当然,由于我们的数据集比较小,特征和歌曲都不够丰富,因此有些推荐结果并不太好。
这段代码可以点此浏览。
如何显示“推荐理由”?
潘多拉在推荐歌曲时会显示推荐理由,我们也可以做到这一点。比如在上面的例子中,我们可以将Magic Potion和Out at Sea的音乐特征做一个比较,找出高度相符的点:
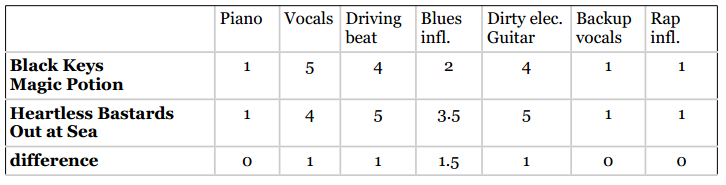
可以看到,两首歌曲最相似的地方是钢琴、和声、以及饶舌,这些特征的差异都是0。但是,这些特征的评分都很低,我们不能告诉用户“因为这首歌曲没有钢琴伴奏,所以我们推荐给你”。因此,我们需要使用那些相似的且评分较高的特征。

我们推荐歌曲是因为它有着强烈的节奏感,美声片段,以及电音吉他的演奏。
评分标准的问题
假如我想增加一种音乐特征——每分钟的鼓点数(bpm),用来判断这是一首快歌还是慢歌。以下是扩充后的数据集:
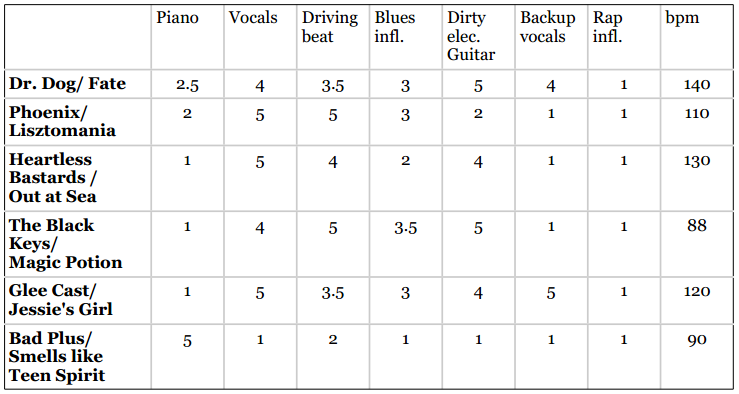
没有bpm时,Magic Potion和Out at Sea距离最近,和Smells Like Teen Spirit距离最远。但引入bpm后,我们的结果就乱套了,因为bpm基本上就决定了两首歌的距离。现在Bad Plus和The Black Keys距离最近就是因为bpm数据相近。
再举个有趣的例子。在婚恋网站上,我通过用户的年龄和收入来进行匹配:
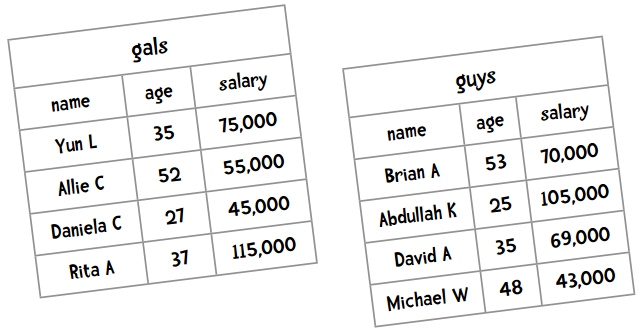
这样一来,年龄的最大差异是28,而薪资的最大差异则是72,000。因为差距悬殊,薪水的高低基本决定了匹配程度。如果单单目测,我们会将David推荐给Yun,因为他们年龄相近,工资也差不多。但如果使用距离计算公式,那么53岁的Brian就会被匹配给Yun,这就不太妙了。

事实上,评分标准不一是所有推荐系统的大敌!
标准化
不用担心,我们可以使用标准化。

要让数据变得可用我们可以对其进行标准化,最常用的方法是将所有数据都转化为0到1之间的值。
拿上面的薪酬数据举例,最大值115,000和最小值43,000相差72,000,要让所有值落到0到1之间,可以将每个值减去最小值,并除以范围(72,000)。所以,Yun标准化之后的薪水是:
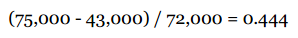
对一些数据集,这种简单的方法效果是不错的。
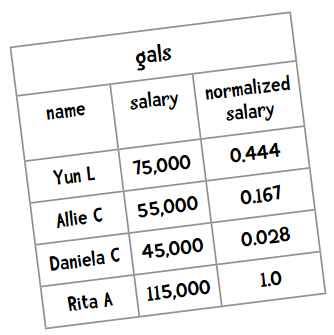
如果你学过统计学,会知道还有其他的标准化方法。比如说标准分(z-score)——分值偏离均值的程度:

标准差的计算公式是:
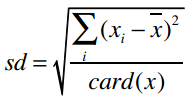
card(x)表示集合x中的元素个数。
如果你对统计学有兴趣,可以读一读《漫话统计学》。
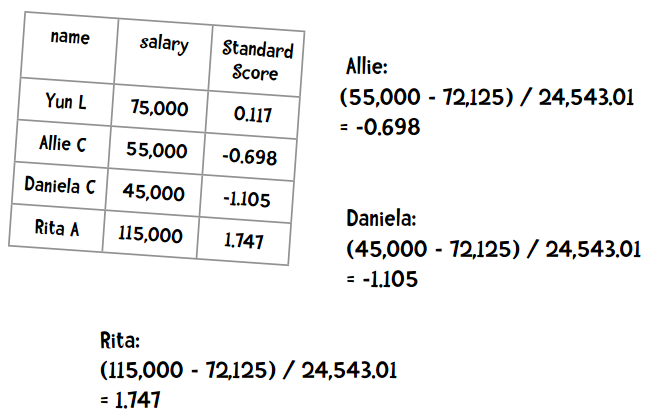
我们用上文中交友网站的数据举例。所有人薪水的总和是577,000,一共有8人,所以均值为72,125。代入标准差的计算公式:
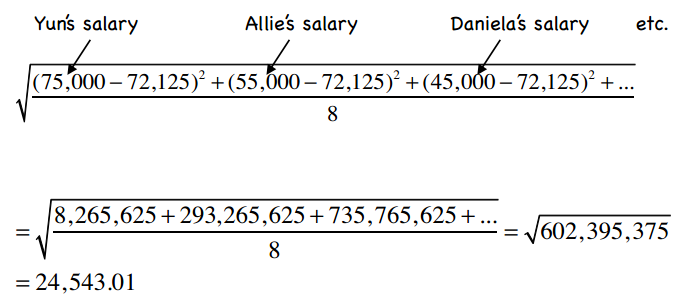
那Yun的标准分则是:
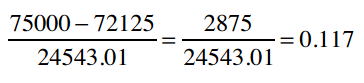
练习题:计算Allie、Daniela、Rita的标准分
标准分带来的问题
标准分的问题在于它会受异常值的影响。比如说一家公司有100名员工,普通员工每小时赚10美元,而CEO一年能赚600万,那全公司的平均时薪为:
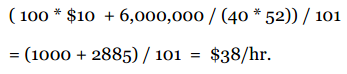
结果是每小时38美元,看起来很美好,但其实并不真实。鉴于这个原因,标准分的计算公式会稍作变化。
修正的标准分
计算方法:将标准分公式中的均值改为中位数,将标准差改为绝对偏差。以下是绝对偏差的计算公式:

中位数指的是将所有数据进行排序,取中间的那个值。如果数据量是偶数,则取中间两个数值的均值。
下面就让我们试试吧。首先将所有人按薪水排序,找到中位数,然后计算绝对偏差:

最后,我们便可以计算得出Yun的修正标准分:
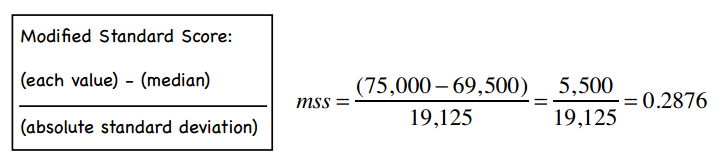
是否需要标准化?
当物品的特征数值尺度不一时,就有必要进行标准化。比如上文中音乐特征里大部分是1到5分,鼓点数却是60到180;交友网站中薪水和年龄这两个尺度也有很大差别。
再比如我想在新墨西哥圣达菲买一处宅子,下表是一些选择:
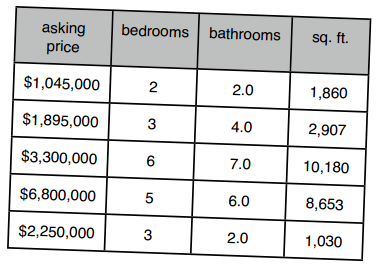
可以看到,价格的范围是最广的,在计算距离时会起到决定性作用;同样,有两间卧室和有二十间卧室,在距离的影响下作用也会很小。
需要进行标准化的情形:
- 我们需要通过物品特性来计算距离;
- 不同特性之间的尺度相差很大。
但对于那种“赞一下”、“踩一脚”的评分数据,就没有必要做标准化了:
在潘多拉的例子中,如果所有的音乐特征都是在1到5分之间浮动的,是否还需要标准化呢?虽然即使做了也不会影响计算结果,但是任何运算都是有性能消耗的,这时我们可以通过比较两种方式的性能和效果来做进一步选择。在下文中,我们会看到标准化反而会降低结果正确性的示例。
回到潘多拉
在潘多拉网站的示例中,我们用一个特征向量来表示一首歌曲,用以计算歌曲的相似度。潘多拉网站同样允许用户对歌曲“赞”和“踩”,那我们要如何利用这些数据呢?
假设我们的歌曲有两个特征,重金属吉他(Dirty Guitar)和强烈的节奏感(Driving Beat),两种特征都在1到5分之间。一位用户对5首歌曲做了“赞”的操作(图中的L),另外五首则“踩”了一下(图中的D):
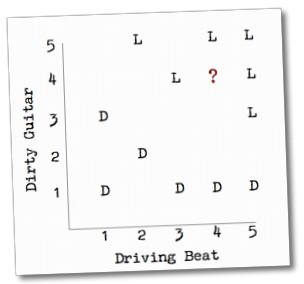
图中多了一个问号所表示的歌曲,你觉得用户会喜欢它还是不喜欢呢?想必你也猜到了,因为这个问号离用户喜欢的歌曲距离较近。这一章接下来的篇幅都会用来讲述这种计算方法。最明显的方式是找到问号歌曲最邻近的歌曲,因为它们之间相似度比较高,再根据用户是否喜欢这些邻近歌曲来判断他对问号歌曲的喜好。
使用Python实现最邻近分类算法
我们仍使用上文中的歌曲示例,用7个特征来标识10首歌曲:

使用Python代码来表示这些数据:
music = {"Dr Dog/Fate": {"piano": 2.5, "vocals": 4, "beat": 3.5, "blues": 3, "guitar": 5, "backup vocals": 4, "rap": 1},
"Phoenix/Lisztomania": {"piano": 2, "vocals": 5, "beat": 5, "blues": 3, "guitar": 2, "backup vocals": 1, "rap": 1},
"Heartless Bastards/Out at Sea": {"piano": 1, "vocals": 5, "beat": 4, "blues": 2, "guitar": 4, "backup vocals": 1, "rap": 1},
"Todd Snider/Don't Tempt Me": {"piano": 4, "vocals": 5, "beat": 4, "blues": 4, "guitar": 1, "backup vocals": 5, "rap": 1},
"The Black Keys/Magic Potion": {"piano": 1, "vocals": 4, "beat": 5, "blues": 3.5, "guitar": 5, "backup vocals": 1, "rap": 1},
"Glee Cast/Jessie's Girl": {"piano": 1, "vocals": 5, "beat": 3.5, "blues": 3, "guitar":4, "backup vocals": 5, "rap": 1},
"La Roux/Bulletproof": {"piano": 5, "vocals": 5, "beat": 4, "blues": 2, "guitar": 1, "backup vocals": 1, "rap": 1},
"Mike Posner": {"piano": 2.5, "vocals": 4, "beat": 4, "blues": 1, "guitar": 1, "backup vocals": 1, "rap": 1},
"Black Eyed Peas/Rock That Body": {"piano": 2, "vocals": 5, "beat": 5, "blues": 1, "guitar": 2, "backup vocals": 2, "rap": 4},
"Lady Gaga/Alejandro": {"piano": 1, "vocals": 5, "beat": 3, "blues": 2, "guitar": 1, "backup vocals": 2, "rap": 1}}
这样做虽然可行,但却比较繁琐,piano、vocals这样的键名需要重复很多次。我们可以将其简化为向量,即Python中的数组类型:
#
# 物品向量中的特征依次为:piano, vocals, beat, blues, guitar, backup vocals, rap
#
items = {"Dr Dog/Fate": [2.5, 4, 3.5, 3, 5, 4, 1],
"Phoenix/Lisztomania": [2, 5, 5, 3, 2, 1, 1],
"Heartless Bastards/Out": [1, 5, 4, 2, 4, 1, 1],
"Todd Snider/Don't Tempt Me": [4, 5, 4, 4, 1, 5, 1],
"The Black Keys/Magic Potion": [1, 4, 5, 3.5, 5, 1, 1],
"Glee Cast/Jessie's Girl": [1, 5, 3.5, 3, 4, 5, 1],
"La Roux/Bulletproof": [5, 5, 4, 2, 1, 1, 1],
"Mike Posner": [2.5, 4, 4, 1, 1, 1, 1],
"Black Eyed Peas/Rock That Body": [2, 5, 5, 1, 2, 2, 4],
"Lady Gaga/Alejandro": [1, 5, 3, 2, 1, 2, 1]}

接下来我还需要将用户“赞”和“踩”的数据也用Python代码表示出来。由于用户并不会对所有的歌曲都做这些操作,所以我用嵌套的字典来表示:
users = {"Angelica": {"Dr Dog/Fate": "L",
"Phoenix/Lisztomania": "L",
"Heartless Bastards/Out at Sea": "D",
"Todd Snider/Don't Tempt Me": "D",
"The Black Keys/Magic Potion": "D",
"Glee Cast/Jessie's Girl": "L",
"La Roux/Bulletproof": "D",
"Mike Posner": "D",
"Black Eyed Peas/Rock That Body": "D",
"Lady Gaga/Alejandro": "L"},
"Bill": {"Dr Dog/Fate": "L",
"Phoenix/Lisztomania": "L",
"Heartless Bastards/Out at Sea": "L",
"Todd Snider/Don't Tempt Me": "D",
"The Black Keys/Magic Potion": "L",
"Glee Cast/Jessie's Girl": "D",
"La Roux/Bulletproof": "D",
"Mike Posner": "D",
"Black Eyed Peas/Rock That Body": "D",
"Lady Gaga/Alejandro": "D"}}
这里使用L和D两个字母来表示喜欢和不喜欢,当然你也可以用其他方式,比如0和1等。
对于新的向量格式,我们需要对曼哈顿距离函数和邻近物品函数做一些调整:
def manhattan(vector1, vector2):
distance = 0
total = 0
n = len(vector1)
for i in range(n):
distance += abs(vector1[i] - vector2[i])
return distance
def computeNearestNeighbor(itemName, itemVector, items):
"""按照距离排序,返回邻近物品列表"""
distances = []
for otherItem in items:
if otherItem != itemName:
distance = manhattan(itemVector, items[otherItem])
distances.append((distance, otherItem))
# 最近的排在前面
distances.sort()
return distances
最后,我需要建立一个分类函数,用来预测用户对一个新物品的喜好,如:
"Chris Cagle/I Breathe In. I Breathe Out" [1, 5, 2.5, 1, 1, 5, 1]
这个函数会先计算出与这个物品距离最近的物品,然后找到用户对这个最近物品的评价,以此作为新物品的预测值。下面是一个最简单的分类函数:
def classify(user, itemName, itemVector):
nearest = computeNearestNeighbor(itemName, itemVector, items)[0][1]
rating = users[user][nearest]
return rating
`
让我们试用一下:
>>> classify('Angelica', 'Chris Cagle/I Breathe In. I Breathe Out', [1, 5, 2.5, 1, 1, 5, 1])
'L'
我们认为她会喜欢这首歌曲!为什么呢?
>>> computeNearestNeighbor('Chris Cagle/I Breathe In. I Breathe Out', [1, 5, 2.5, 1, 1, 5, 1], items)
[(4.5, 'Lady Gaga/Alejandro'), (6.0, "Glee Cast/Jessie's Girl"), (7.5, "Todd Snider/Don't Tempt Me"), (8.0, 'Mike Posner'), (9.5, 'Heartless Bastards/Out'), (10.5, 'Black Eyed Peas/Rock That Body'), (10.5, 'Dr Dog/Fate'), (10.5, 'La Roux/Bulletproof'), (10.5, 'Phoenix/Lisztomania'), (14.0, 'The Black Keys/Magic Potion')]
可以看到,距离I Breathe In最近的歌曲是Alejandro,并且Angelica是喜欢这首歌曲的,所以我们预测她也会喜欢I Breathe In。
其实我们做的是一个分类器,将歌曲分为了用户喜欢和不喜欢两个类别。
号外,号外!我们编写了一个分类器!

分类器是指通过物品特征来判断它应该属于哪个组或类别的程序!
分类器程序会基于一组已经做过分类的物品进行学习,从而判断新物品的所属类别。在上面的例子中,我们知道Angelica喜欢和不喜欢的歌曲,然后据此判断她是否会喜欢Chris Cagle的歌。
- 在Angelica评价过的歌曲中找到距离Chris Cagle最近的歌曲,即Laydy Gaga的Alejandro;
- 由于Angelica是喜欢Alejandro这首歌的,所以我们预测她也会喜欢Chris Cagle的Breathe In, Breathe Out。
分类器的应用范围很广,以下是一些示例:
推特情感分类
很多人在对推特中的文字消息进行情感分类(积极的、消极的),可以有很多用途,如Axe发布了一款新的腋下除臭剂,通过推文就能知道用户是否满意。这里用到的物品特征是文字信息。
人脸识别
现在有些手机应用可以识别出照片里你的朋友们,这项技术也可用于监控录像中的人脸识别。不同的识别技术细节可能不同,但都会用到诸如五官的大小和相对距离等信息。
政治拉票
通过将目标选民分为“爱凑热闹”、“很有主见”、“家庭为重”等类型,来进行有针对性的拉票活动。
市场细分
这和上个例子有点像,与其花费巨额广告费向不可能购买维加斯公寓的人进行宣传,不如从人群中识别出潜在客户,缩小宣传范围。最好能再对目标群体进行细分,进一步定制广告内容。
个人健康助理
如今人们越来越关注自身,我们可以购买到像Nike健身手环这样的产品,而Intel等公司也在研制一种智能家居,可以在你行走时称出你的重量,记录你的行动轨迹,并给出健康提示。有些专家还预言未来我们会穿戴各种便携式设备,收集我们的生活信息,并加以分类。
其他
- 识别恐怖分子
- 来信分类(重要的、一般的、垃圾邮件)
- 预测医疗费用
- 识别金融诈骗
她是从事什么运动的?
让我们来为之后的几章做一个预热,先看一个较为简单的例子——根据女运动员的身高和体重来判断她们是从事什么运动项目的。下表是原始数据:
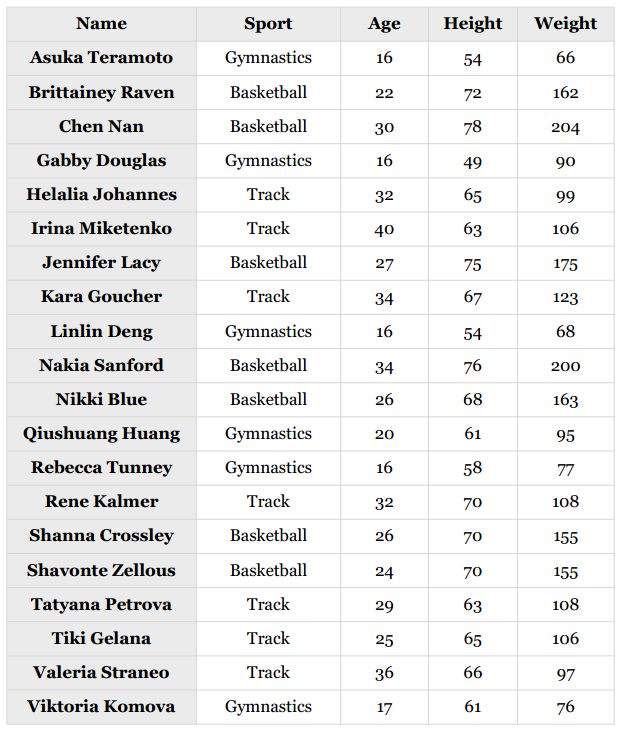
这里列出的是2008和2012奥运会上排名靠前的二十位女运动员。篮球运动员参加了WNBA;田径运动员则完成了2012年奥运会的马拉松赛。虽然数据量很小,但我们仍可以对其应用一些数据挖掘算法。
你可以看到上表中列出了运动员的年龄,光凭这一信息就能进行一些预测了。比如,以下运动员会是哪个项目的呢?

答案
Candace Parker是篮球运动员,McKayla Maroney是美国女子体操队的一员,Olivera Jevtic是塞尔维亚的一名长跑运动员,Lisa Jane Weightman则是澳大利亚的长跑运动员。
看,我们刚刚就进行了一次分类——通过运动员的年龄特征来识别她们参与的体育项目。
头脑风暴
假设我想通过运动员的身高和体重来预测她所从事的运动,数据集只有两人:Nakia Sanford是篮球运动员,身高6尺4寸(76英寸,1.93米),体重200磅(90公斤);Sarah Beale是橄榄球运动员,身高5尺10寸(70英寸,1.78米),体重190磅(86公斤)。我想知道Catherine Spencer是从事哪项运动的,她的身高是5尺10寸,重200磅,如何预测呢?
如果你认为她是橄榄球运动员,那么你猜对了。但是,如果用曼哈顿距离来进行计算,Catherine和Nakia的距离是6,和Sarah的距离是10,那应该预测她是篮球运动员才对。我们之前是否学过一个方法,能让距离计算更为准确呢?
没错,就是修正的标准分!
测试数据
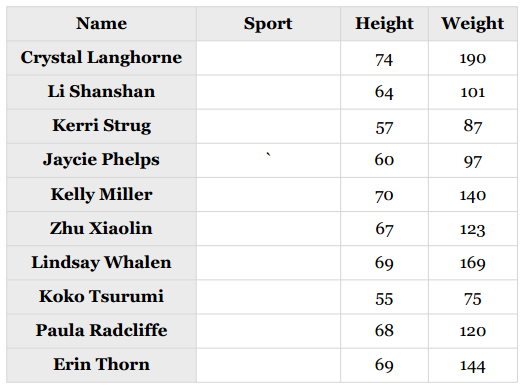
下表是我们需要进行预测的运动员列表,一起来做分类器吧!
Python编码
这次我们不将数据直接写在Python代码中,而是放到两个文本文件里:athletesTrainingSet.txt和athletesTestSet.txt。我会使用第一个文件中的数据来训练分类器,然后使用测试文件里的数据来进行评价。
文件格式大致如下:

文件中的每一行是一条完整的记录,字段使用制表符分隔。我要使用运动员的身高体重数据来预测她所从事的运动项目,也就是用第三、四列的数据来预测第二列的数据。运动员的姓名不会使用到,我们既不能通过运动员的姓名得知她参与的项目,也不会通过身高体重来预测运动员的姓名。

你好,你有五英尺高,150磅重,莫非你的名字是Clara Coleman?
当然,名字也有它的用处,我们可以用它来解释分类器的预测结果:“我们认为Amelia Pond是一名体操运动员,因为她的身高体重和另一名体操运动员Gabby Douglas很接近。”
为了让我们的Python代码更具一般性,并不只适用于这一种数据集,我会为每一列数据增加一个列名,如:

所有被标记为comment的列都会被分类器忽略;标记为class的列表示物品所属分类;不定个数的num列则表示物品的特征。
头脑风暴
我们在Python中应该如何表示这些数据呢?以下是一些可能性:
# 1
{'Asuka Termoto': ('Gymnastics', [54, 66]),
'Brittainey Raven': ('Basketball', [72, 162]), ...
这种方式使用了运动员的姓名作为键,而我们说过分类器程序根本不会使用到姓名,所以不合理。
# 2
[['Asuka Termoto', 'Gymnastics', 54, 66],
['Brittainey Raven', 'Basketball', 72, 162], ...
这种方式看起来不错,它直接反映了文件的格式。由于我们需要遍历文件的数据,所以使用列表类型(list)是合理的。
# 3
[('Gymnastics', [54, 66], ['Asuka Termoto']),
('Basketball', [72, 162], ['Brittainey Raven']), ...
这是我最认同的表示方式,因为它将不同类型的数据区别开来了,依次是分类、特征、备注。这里备注可能有多个,所以也用了一个列表来表示。以下是读取数据文件并转换成上述格式的函数:
class Classifier:
def __init__(self, filename):
self.medianAndDeviation = []
# 读取文件
f = open(filename)
lines = f.readlines()
f.close()
self.format = lines[0].strip().split('\t')
self.data = []
for line in lines[1:]:
fields = line.strip().split('\t')
ignore = []
vector = []
for i in range(len(fields)):
if self.format[i] == 'num':
vector.append(int(fields[i]))
elif self.format[i] == 'comment':
ignore.append(fields[i])
elif self.format[i] == 'class':
classification = fields[i]
self.data.append((classification, vector, ignore))
动手实践
在计算修正的标准分之前,我们需要编写获取中位数和计算绝对偏差的函数,尝试实现这两个函数:
>>> heights = [54, 72, 78, 49, 65, 63, 75, 67, 54]
>>> median = classifier.getMedian(heights)
>>> median
65
>>> asd = classifier.getAbsoluteStandardDeviation(heights, median)
>>> asd
8.0
关于断言
通常我们会将一个大的算法拆分成几个小的组件,并为每个组件编写一些单元测试,从而确保它能正常工作。很多时候,我们会先写单元测试,再写正式的代码。在我提供的模板代码中已经编写了一些单元测试,摘录如下:
def unitTest():
list1 = [54, 72, 78, 49, 65, 63, 75, 67, 54]
classifier = Classifier('athletesTrainingSet.txt')
m1 = classifier.getMedian(list1)
assert(round(m1, 3) == 65)
...
print("getMedian和getAbsoluteStandardDeviation均能正常工作")
你需要完成的geMedian函数的模板是:
def getMedian(self, alist):
"""返回中位数"""
"""请在此处编写代码"""
return 0
这个模板函数返回的是0,你需要编写代码来返回列表的中位数。比如单元测试中我传入了以下列表:
[54, 72, 78, 49, 65, 63, 75, 67, 54]
assert(断言)表示函数的返回值应该是65。如果所有的单元测试都能通过,则报告以下信息:
getMedian和getAbsoluteStandardDeviation均能正常工作
否则,则抛出以下异常:
File "testMedianAndASD.py", line 78, in unitTest
assert(round(m1, 3) == 65)
AssertError
断言在单元测试中是很常用的。
将大型代码拆分成一个个小的部分,并为每个部分编写单元测试,这一点是很重要的。如果没有单元测试,你将无法知道自己是否正确完成了所有任务,以及未来的某个修改是否会导致你的程序不可用。--- Peter Norvig

答案
def getMedian(self, alist):
"""返回中位数"""
if alist == []:
return []
blist = sorted(alist)
length = len(alist)
if length % 2 == 1:
# 列表有奇数个元素,返回中间的元素
return blist[int(((length + 1) / 2) - 1)]
else:
# 列表有偶数个元素,返回中间两个元素的均值
v1 = blist[int(length / 2)]
v2 =blist[(int(length / 2) - 1)]
return (v1 + v2) / 2.0
def getAbsoluteStandardDeviation(self, alist, median):
"""计算绝对偏差"""
sum = 0
for item in alist:
sum += abs(item - median)
return sum / len(alist)
可以看到,getMedian函数对列表进行了排序,由于数据量并不大,所以这种方式是可以接受的。如果要对代码进行优化,我们可以使用选择算法。
现在,我们已经将数据从athletesTrainingSet.txt读取出来,并保存为以下形式:
[('Gymnastics', [54, 66], ['Asuka Teramoto']),
('Basketball', [72, 162], ['Brittainey Raven']),
('Basketball', [78, 204], ['Chen Nan']),
('Gymnastics', [49, 90], ['Gabby Douglas']), ...
我们需要对向量中的数据进行标准化,变成以下结果:
[('Gymnastics', [-1.93277, -1.21842], ['Asuka Teramoto']),
('Basketball', [1.09243, 1.63447], ['Brittainey Raven']),
('Basketball', [2.10084, 2.88261], ['Chen Nan']),
('Gymnastics', [-2.7731, -0.50520],
('Track', [-0.08403, -0.23774], ['Helalia Johannes']),
('Track', [-0.42017, -0.02972], ['Irina Miketenko']), ...
在init方法中,添加标准化过程:
# 获取向量的长度
self.vlen = len(self.data[0][1])
# 标准化
for i in range(self.vlen):
self.normalizeColumn(i)
在for循环中逐列进行标准化,即第一次会标准化身高,第二次标准化体重。
动手实践 下载normalizeColumnTemplate.py文件,编写normalizeColumn方法。
答案
def normalizeColumn(self, columnNumber):
"""标准化self.data中的第columnNumber列"""
# 将该列的所有值提取到一个列表中
col = [v[1][columnNumber] for v in self.data]
median = self.getMedian(col)
asd = self.getAbsoluteStandardDeviation(col, median)
#print("Median: %f ASD = %f" % (median, asd))
self.medianAndDeviation.append((median, asd))
for v in self.data:
v[1][columnNumber] = (v[1][columnNumber] - median) / asd
可以看到,我将计算得到的中位数和绝对偏差保存在了medianAndDeviation变量中,因为我们会用它来标准化需要预测的向量。比如,我要预测Kelly Miller的运动项目,她身高5尺10寸(70英寸),重140磅,即原始向量为[70, 140],需要先进行标准化。
我们计算得到的meanAndDeviation为:
[(65.5, 5.95), (107.0, 33.65)]
它表示向量中第一元素的中位数为65.5,绝对偏差为5.95;第二个元素的中位数为107.0,绝对偏差33.65。
现在我们就利用这组数据将[70, 140]进行标准化。第一个元素的标准分数是:
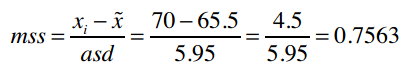
第二个元素为:
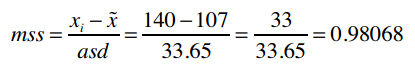
以下是实现它的Python代码:
def normalizeVector(self, v):
"""我们已保存了每列的中位数和绝对偏差,现用它来标准化向量v"""
vector = list(v)
for i in range(len(vector)):
(median, asd) = self.medianAndDeviation[i]
vector[i] = (vector[i] - median) / asd
return vector
最后,我们要编写分类函数,用来预测运动员的项目:
classifier.classify([70, 140])
在我们的实现中,classify函数只是nearestNeighbor的一层包装:
def classify(self, itemVector):
"""预测itemVector的分类"""
return self.nearestNeighbor(self.normalizeVector(itemVector))[1][0]
动手实践 实现nearestNeighbor函数。
答案
def manhattan(self, vector1, vector2):
"""计算曼哈顿距离"""
return sum(map(lambda v1, v2: abs(v1 - v2), vector1, vector2))
def nearestNeighbor(self, itemVector):
"""返回itemVector的近邻"""
return min([(self.manhattan(itemVector, item[1]), item)
for item in self.data])
好了,我们用200多行代码实现了近邻分类器!

在完整的示例代码中,我提供了一个test函数,它可以对分类器程序的准确性做一个评价。比如用它来评价上面实现的分类器:
- Track Aly Raisman Gymnastics 62 115
+ Basketball Crystal Langhorne Basketball 74 190
+ Basketball Diana Taurasi Basketball 72 163
...
+ Track Xueqin Wang Track 64 110
+ Track Zhu Xiaolin Track 67 123
80.00% correct
可以看到,这个分类器的准确率是80%。它对篮球运动员的预测很准确,但在预测田径和体操运动员时出现了4个失误。
鸢尾花数据集
我们可以用鸢尾花数据集做测试,这个数据集在数据挖掘领域是比较有名的。它是20世纪30年代Ronald Fisher对三种鸢尾花的50个样本做的测量数据(萼片和花瓣)。

Ronald Fisher是一名伟大的科学家。他对统计学做出了革命性的改进,Richard Dawkins称他为“继达尔文后最伟大生物学家。”

鸢尾花数据集可以在这里找到,你可以测试你的算法,并问自己一些问题:标准化让结果更正确了吗?训练集中的数据量越多越好吗?用欧几里得距离来算会怎样?
记住 所有的学习过程都是在你自己的脑中进行的,你付出的努力越多,学到的也就越多。
鸢尾花数据集的格式如下,我们要预测的是Species这一列:
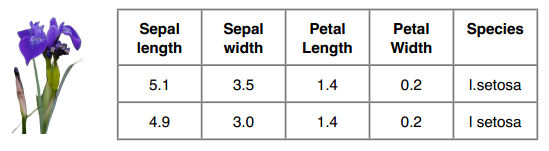
训练集中有120条数据,测试集中有30条,两者没有交集。
测试结果如何呢?
>>> test('irisTrainingSet.data', 'iristestSet.data')
93.33% correct
这又一次证明我们的分类算法是简单有效的。有趣的是,如果不对数据进行标准化,它的准确率将达到100%。这个现象我们会在后续的章节中讨论。
每加仑燃油可以跑多少公里?
最后,我们再来测试另一个广泛使用的数据集,卡内基梅隆大学统计的汽车燃油消耗和公里数数据。它在1983年的美国统计联合会展中使用过,大致格式如下:
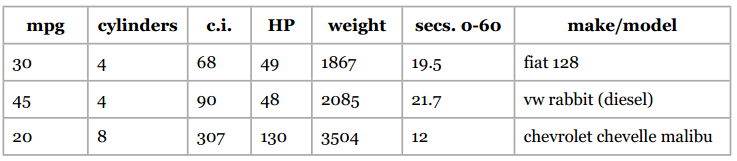
这个数据集做过一些修改。我们要预测的是加仑燃油公里数(mpg),使用的数据包括汽缸数、排气量、马力、重量、加速度等。

数据集中有342条记录,50条测试记录,运行结果如下:
>>> test('mpgTrainingSet.txt', 'mpgTestSet.txt')
56.00% correct
如果不进行标准化,准确率将只有32%。

我们应该如何提高预测的准确率呢?改进分类算法?增加训练集?还是增加特征的数量?我们将在下一章揭晓!
番外篇:关于标准化
这一章我们讲解了标准化的重要性,即当不同特征的评分尺度不一致时,为了得到更准确的距离结果,就需要将这些特征进行标准化,使他们在同一个尺度内波动。

虽然大多数数据挖掘工程师对标准化的理解是一致的,但也有一些人要将这种做法区分为“正规化”和“标准化”两种。其中,“正规化”表示将值的范围缩小到0和1之间;“标准化”则是将特征值转换为均值为0的一组数,其中每个数表示偏离均值的程度(即标准偏差或绝对偏差)。我们使用的修正的标准分就是属于后者。
回忆一下,我们上文中有讲解过如何将特征值缩小到0到1之间:找出最大最小值,并做如下计算:
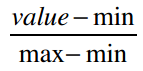
我们来比较一下使用不同的标准化方法得到的准确度:
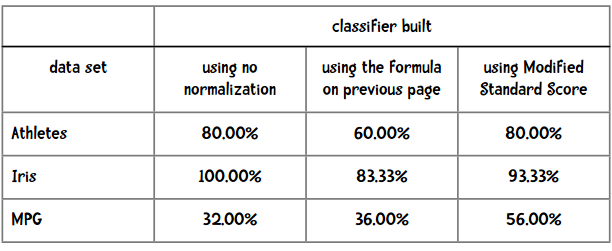
看来还是使用修正的标准分结果会好些。

用不同的数据集来测试我们的算法是不是很有趣?这些数据集是从UCI机器学习仓库中获得的。去下载一些新的数据集,调整一下格式,测试我们学过的算法吧!